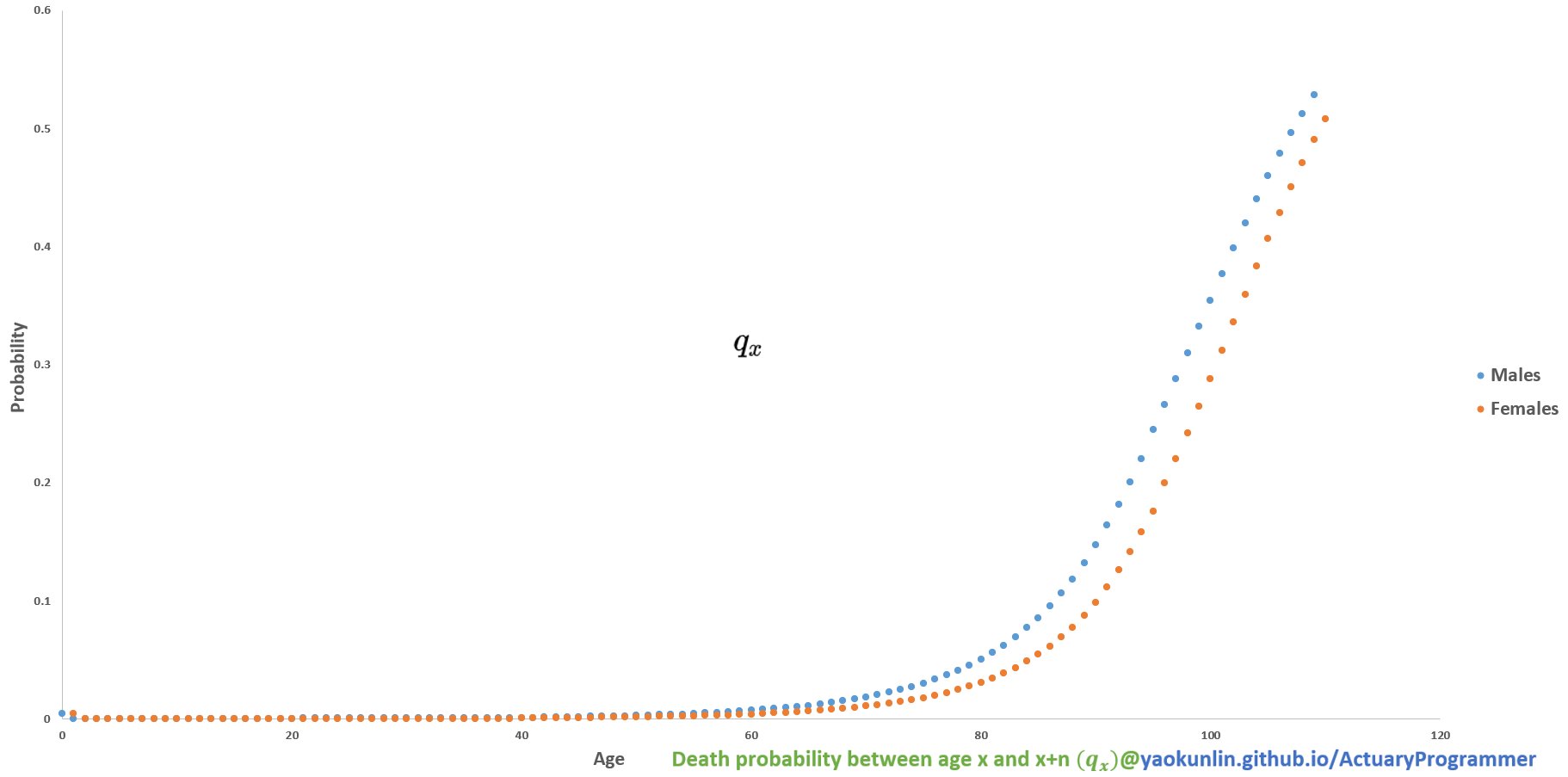
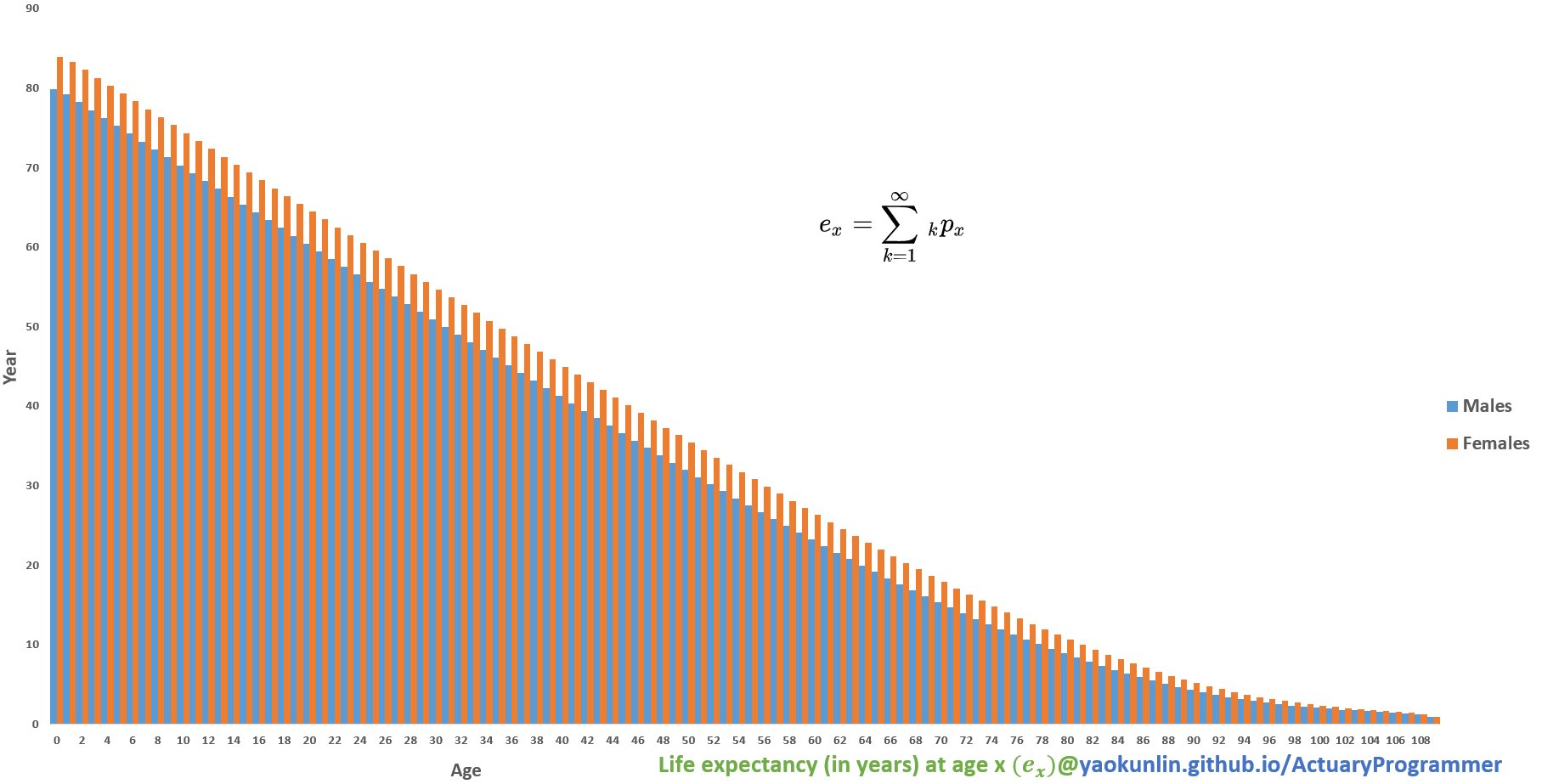
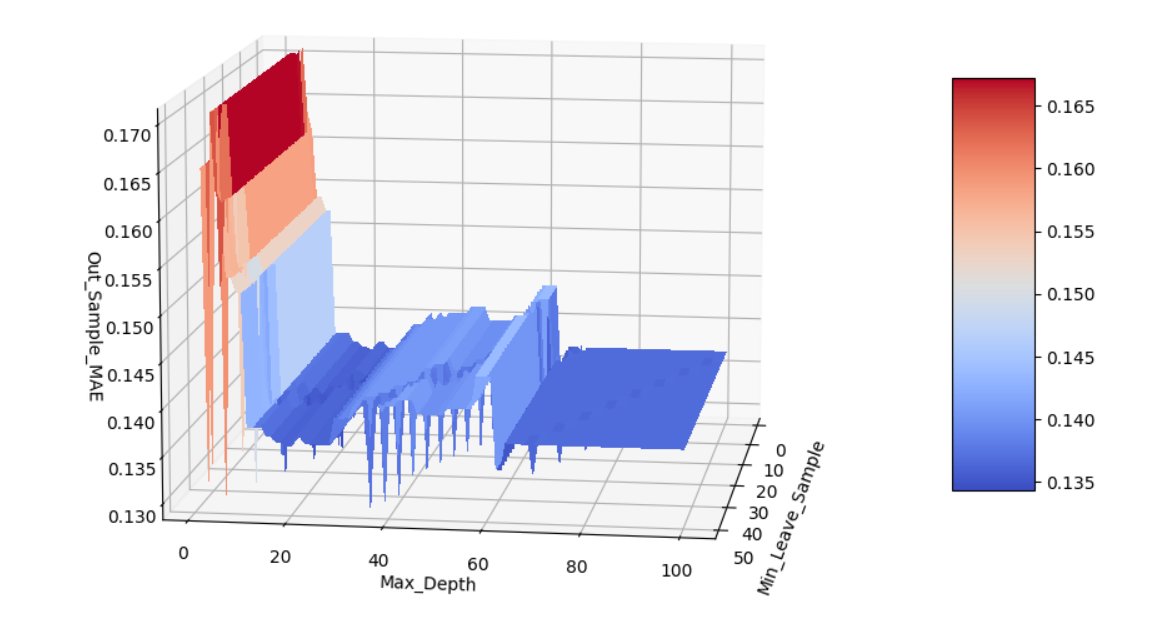
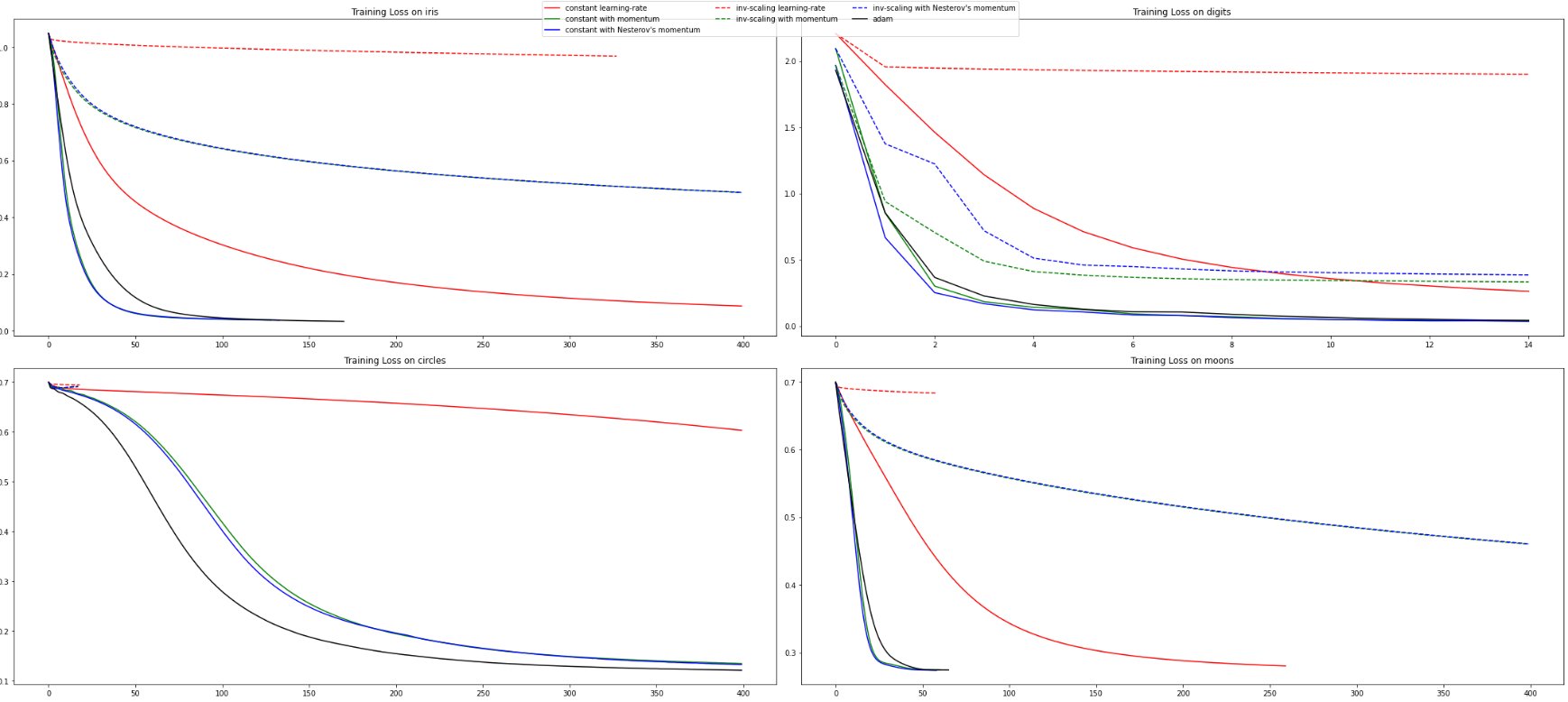
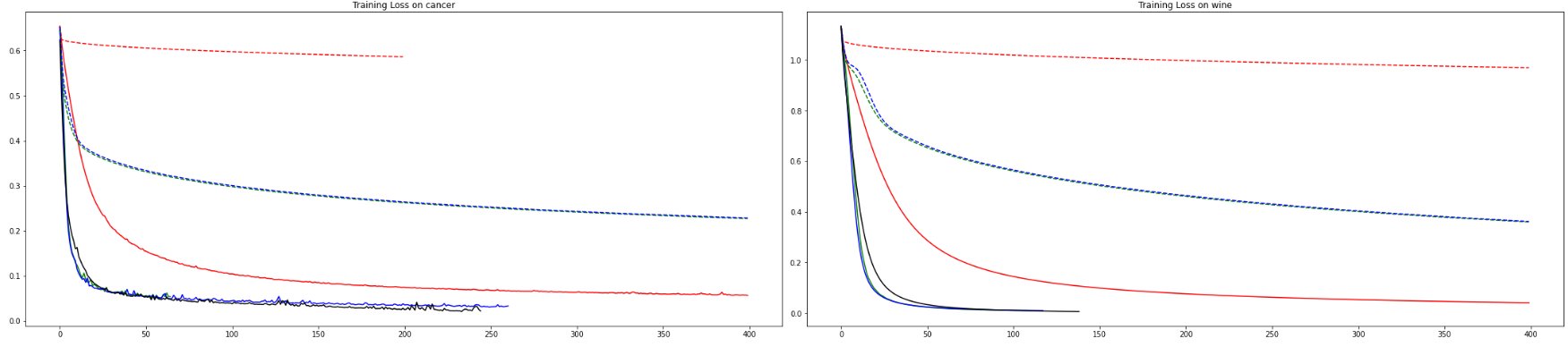
-
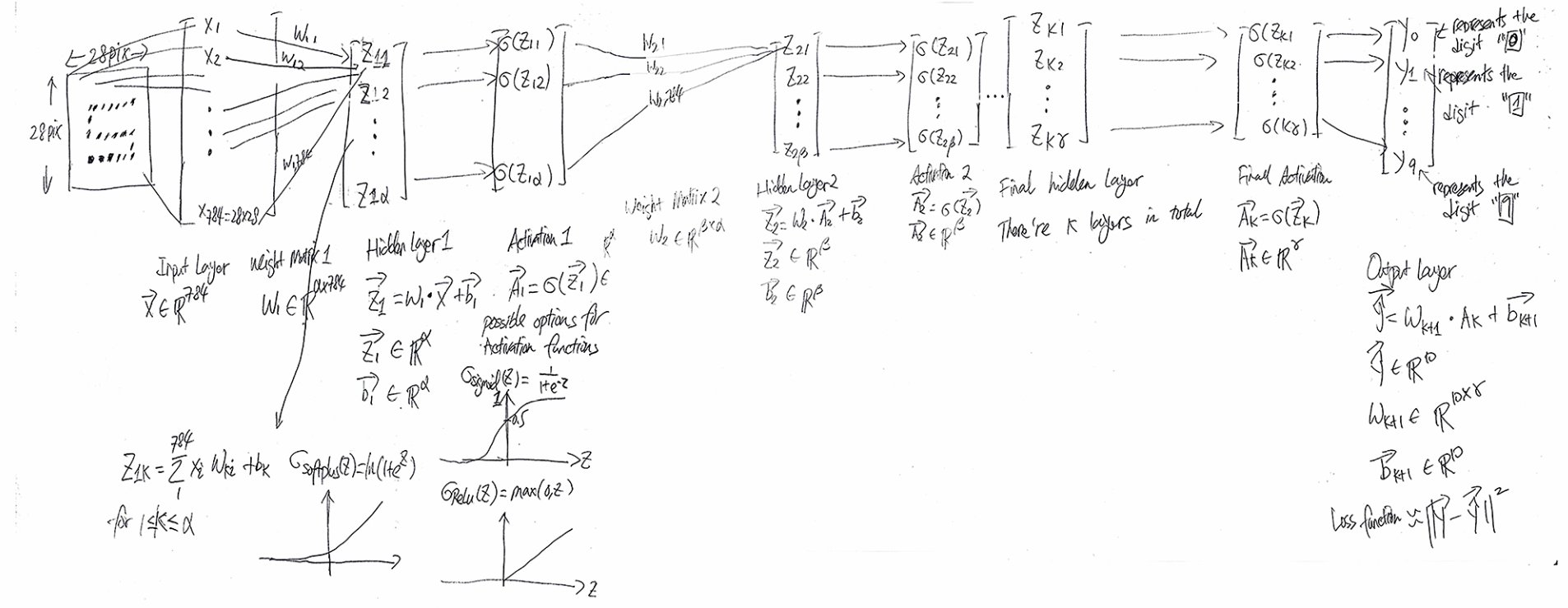
- The above draft note demonstrates the feedforward process for one image:
-
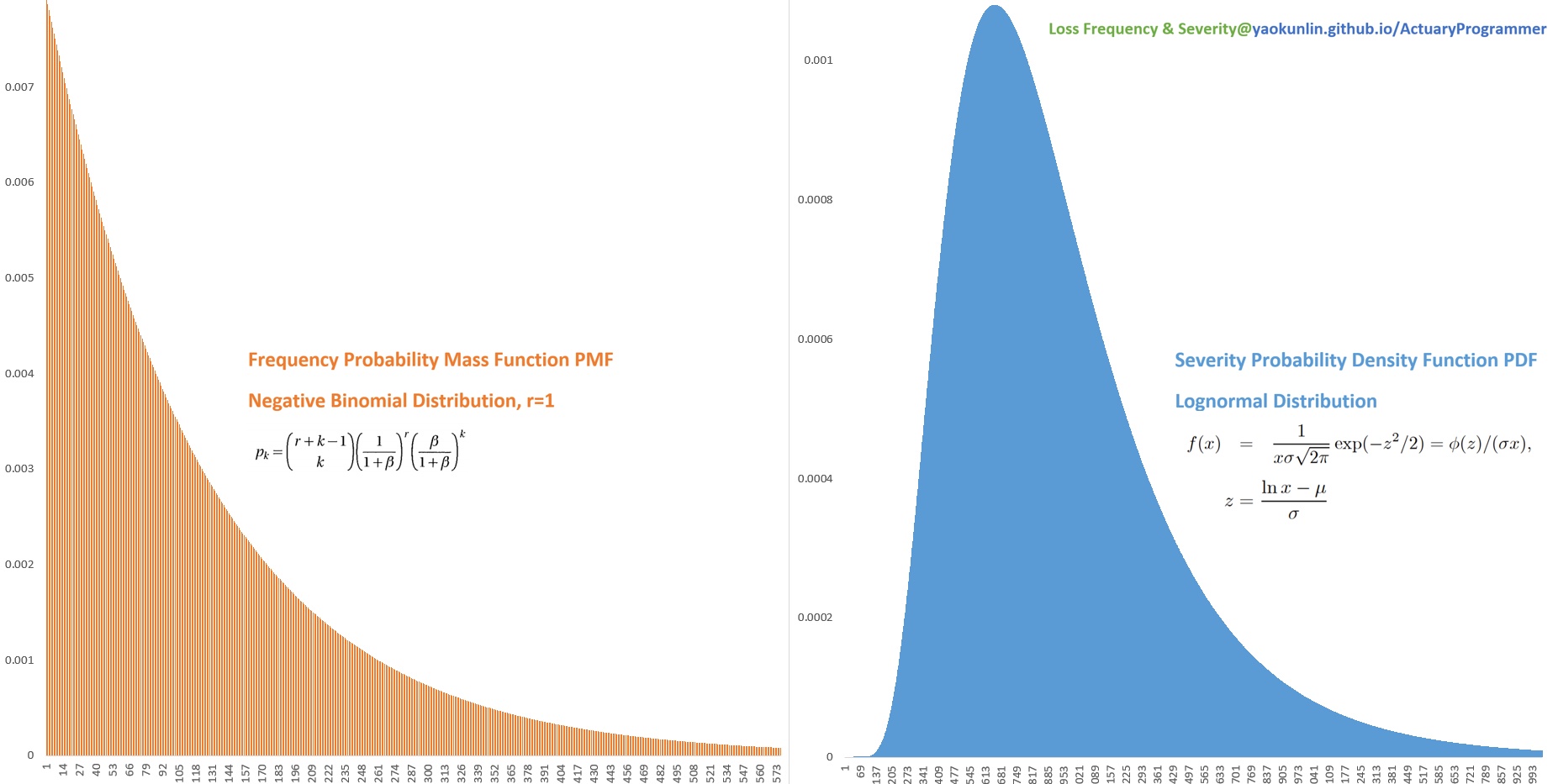
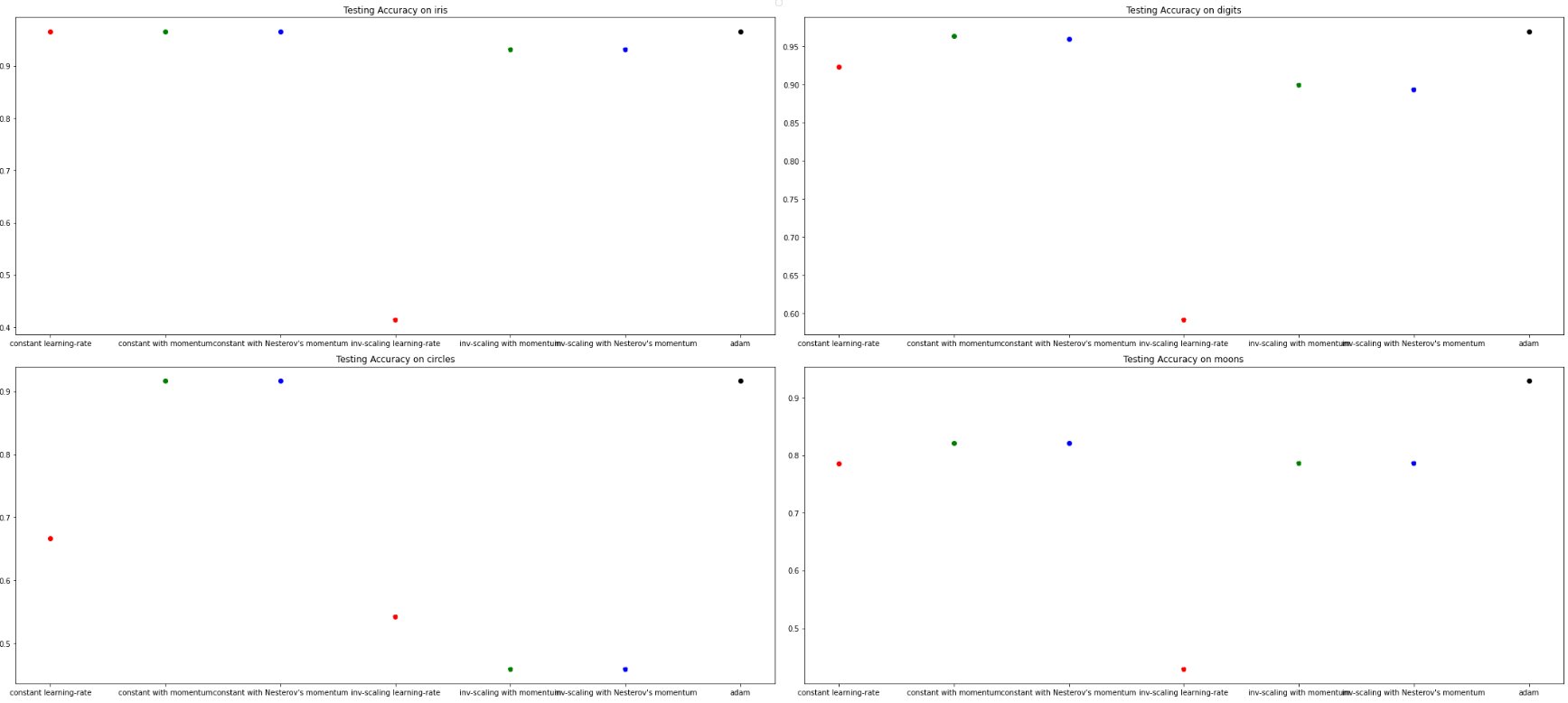
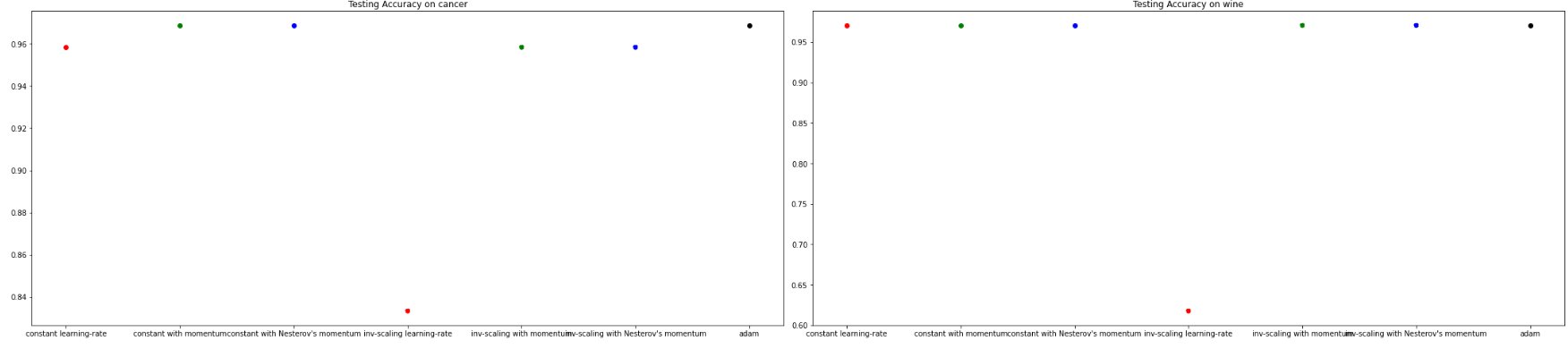
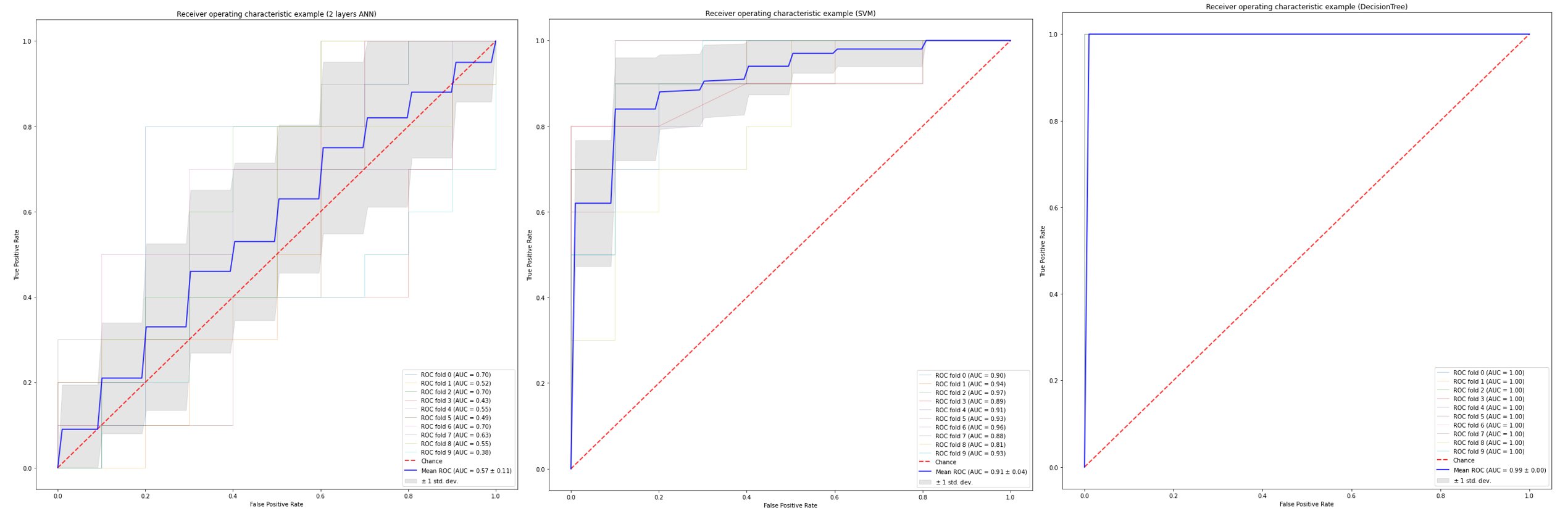
Each grayscale handwritten digit image has 28 (width) × 28 (height) × 1 (color) pixels; this information is translated into a 784 × 1 vector
(shown on the left left-hand of the draft note)
Perform matrix multiplication between the first weight matrix W1 and the input vector (which is 784 × 1) and add the first bias vector b1, then transform the resulting vector by an activation function (some popular activation functions include: Rectified Linear Unit ReLu, Sigmoid function, Softplus function)
Z1 = W1 × Input Vector + b1
Activation1 = σ1 (Z1), where σ1(*) is the activation function for the first hidden layer, and the operation performs element-wise.
Activation1 is the output of the first hidden layer which will be the input of the second hidden layer.
Z2 = W2 × Activation1 + b2
Activation2 = σ2 (Z2), where σ2(*) is the activation function for the second hidden layer, which does not need to be the same as σ1(*).
Activation2 is the output of the second hidden layer which will be the input of the third hidden layer.
... ...Zlast = Wlast × Activationlast-1 + blast
Wlast is the last weight matrix , blast is the last bias vector
Activationlast = σlast (Zlast-1)
Activationlast is the output layer which is a 10 × 1 vector, this vector dimension is due to there are total 10 digits (from 0 to 9).
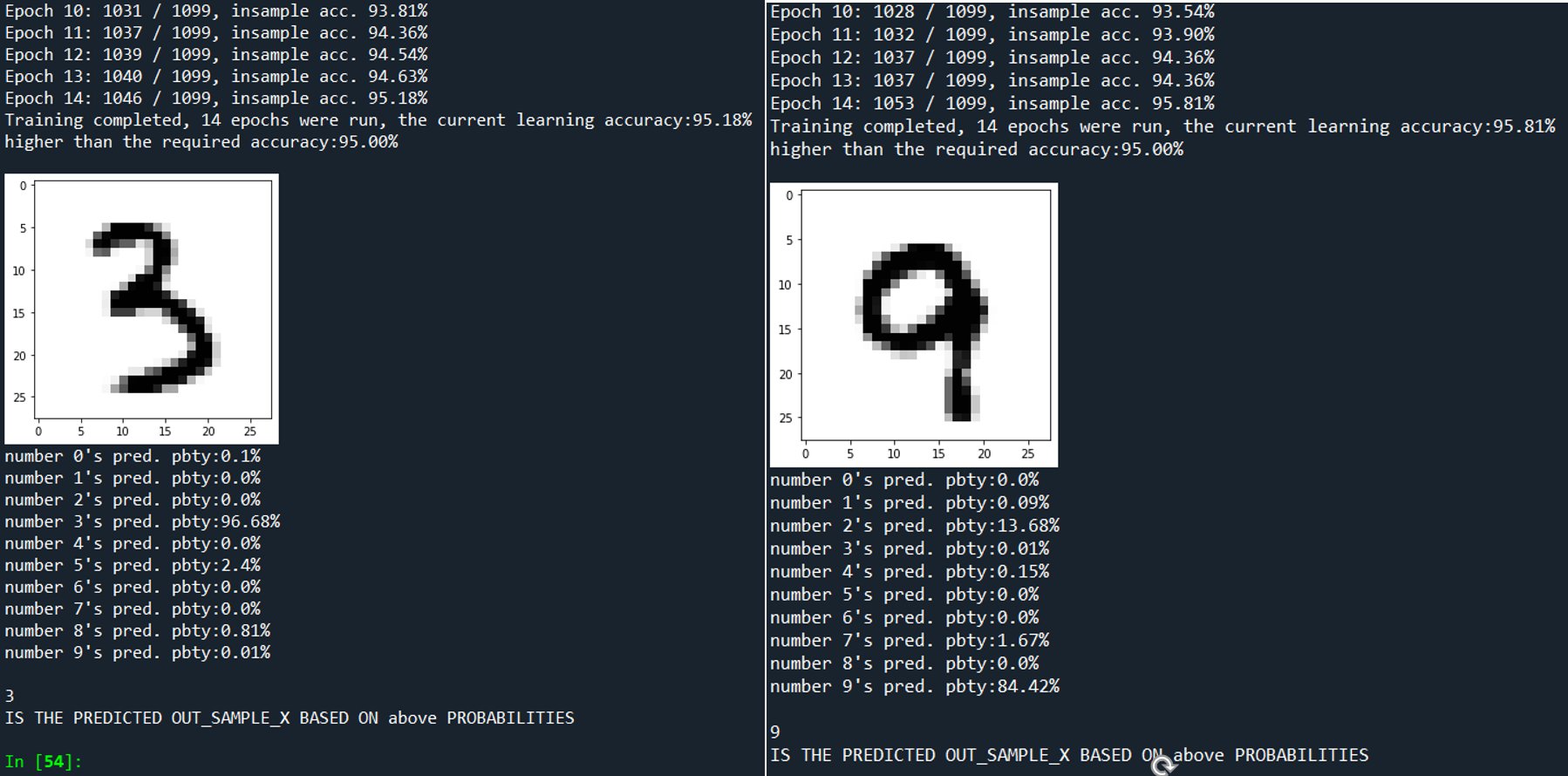
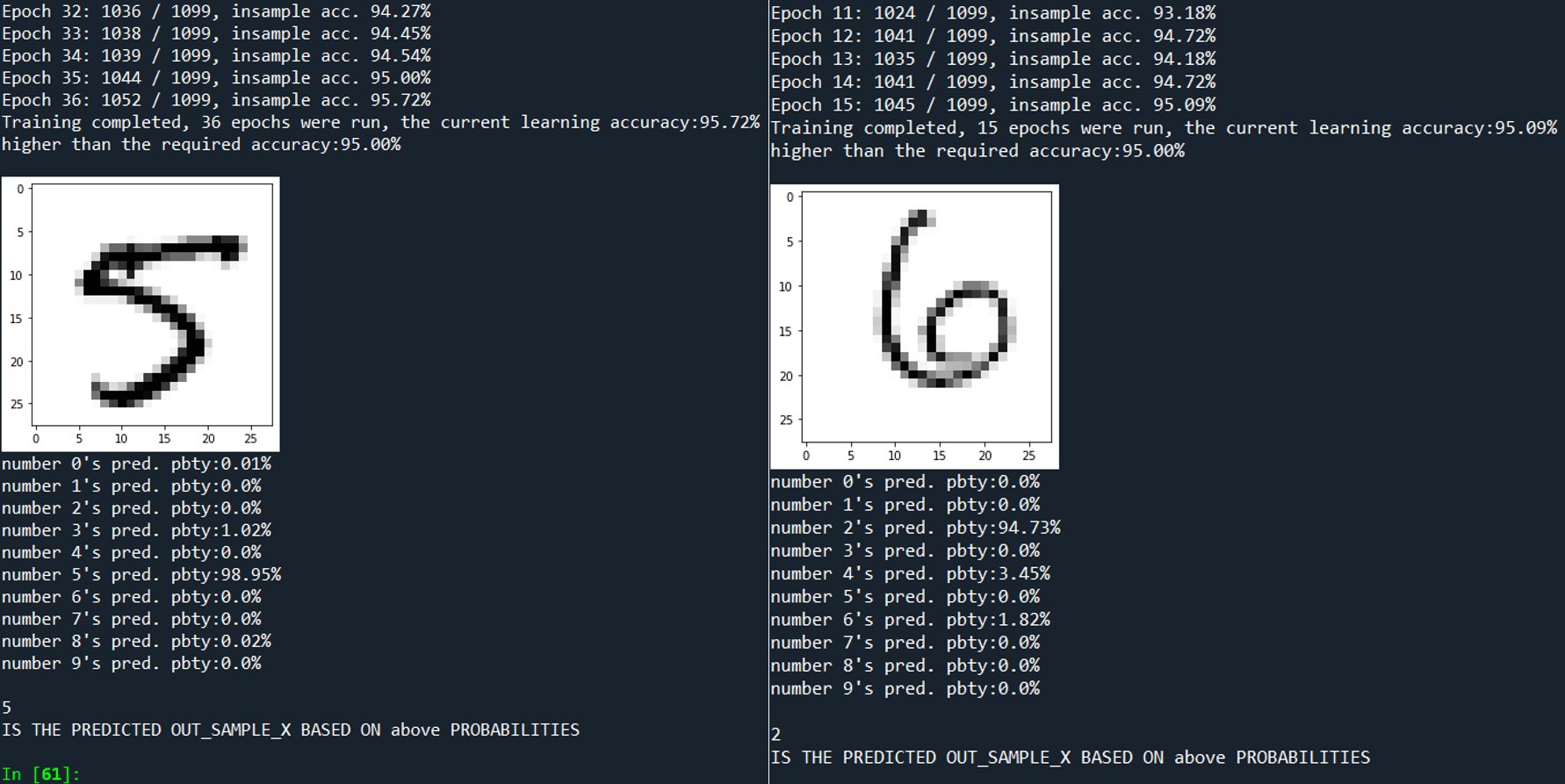
- ......
- ......
Welcome to my warehouse.
This blog started from some projects and notes I made for myself. I hope you like the posts, comments are always welcome.
(Shhhh... bonus content sitting at the end of this website)
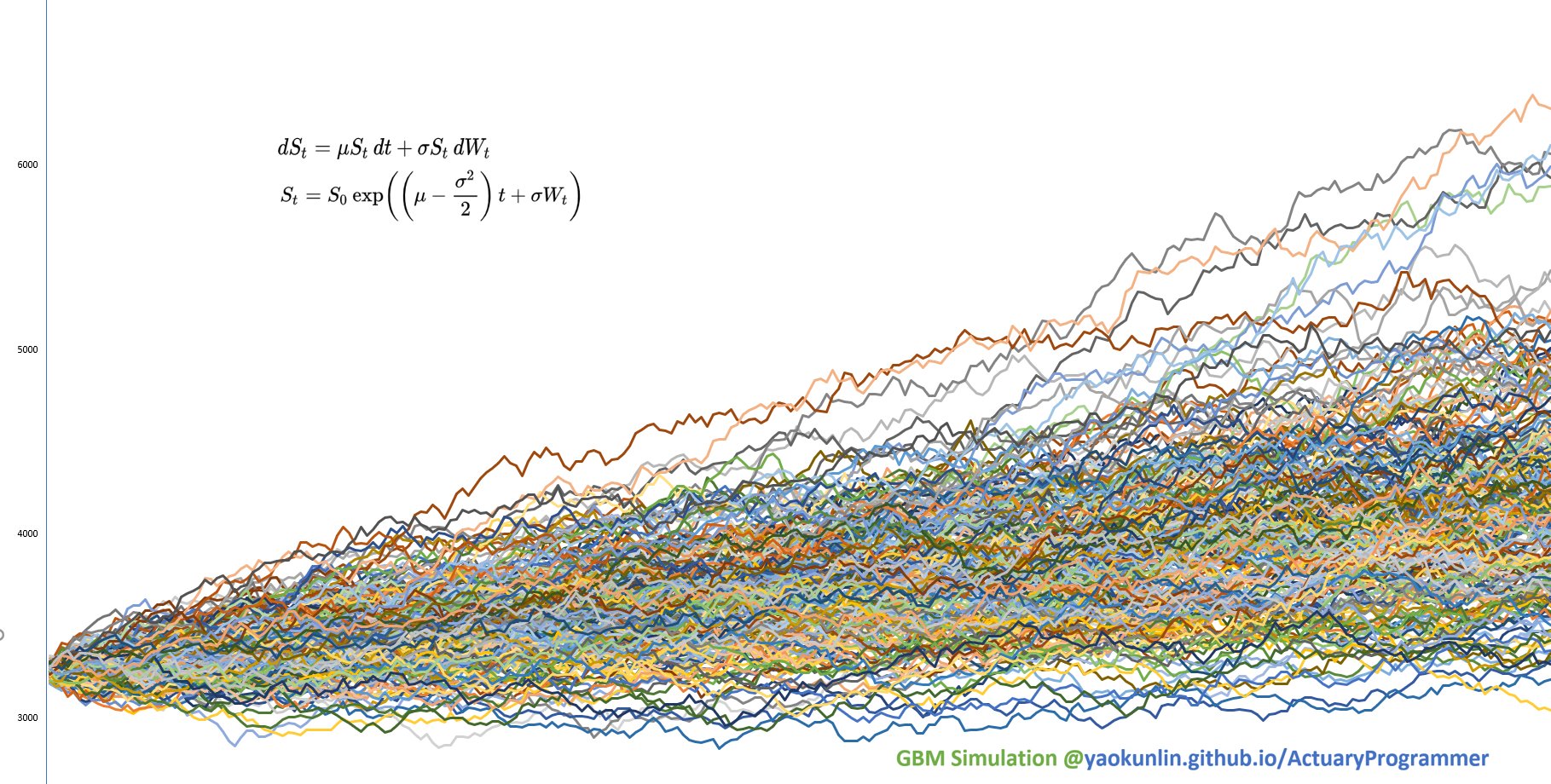
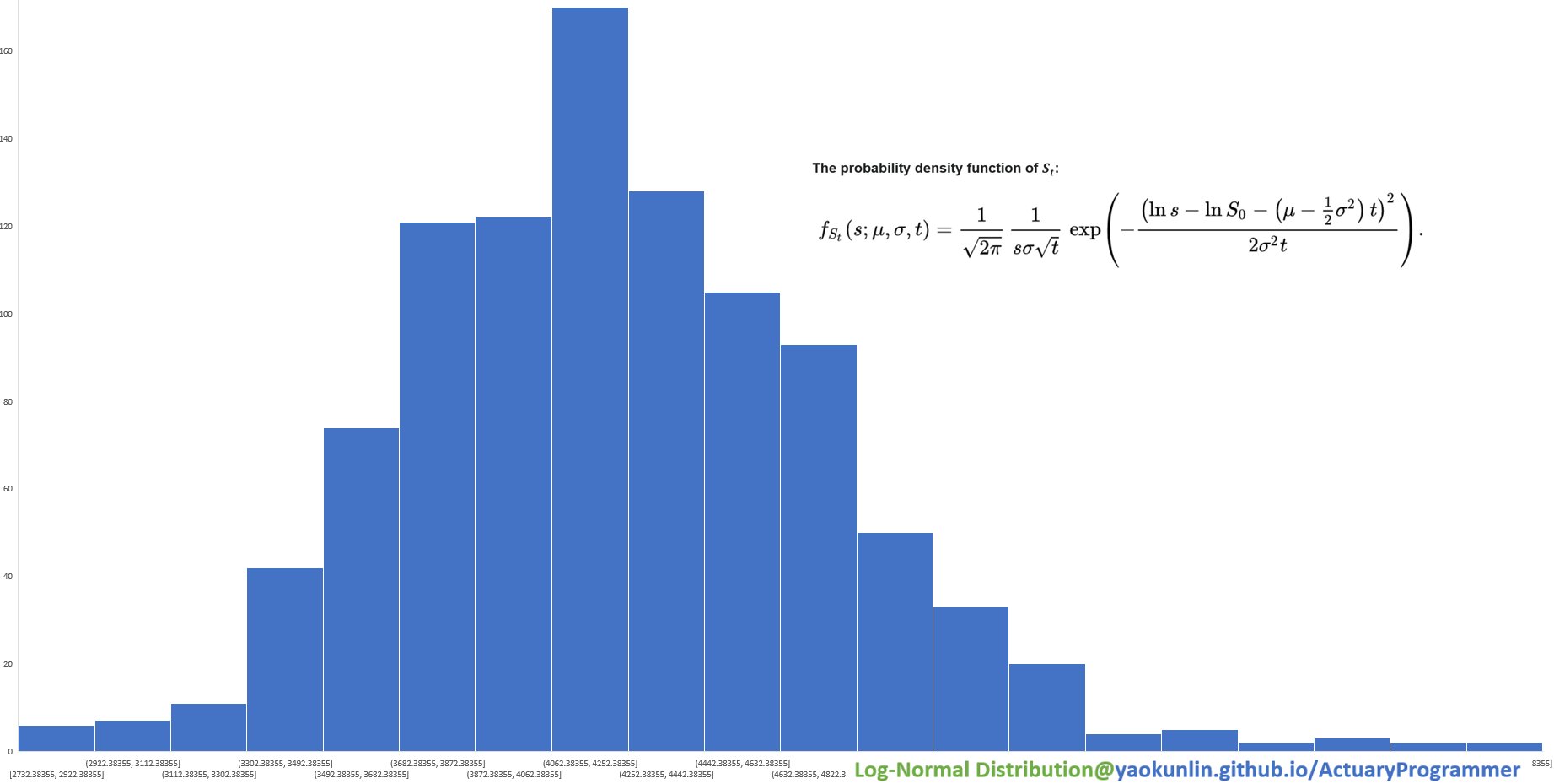
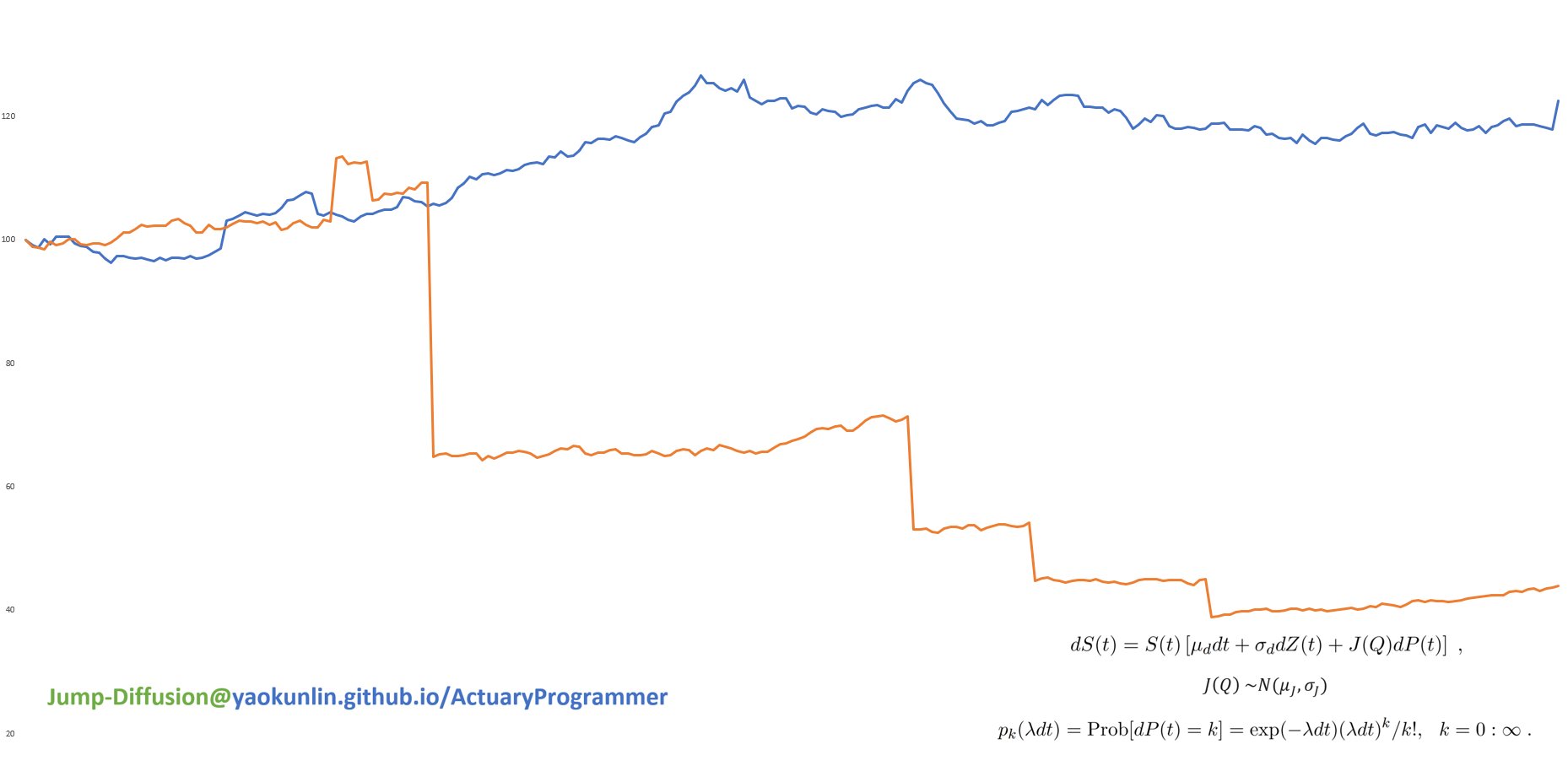
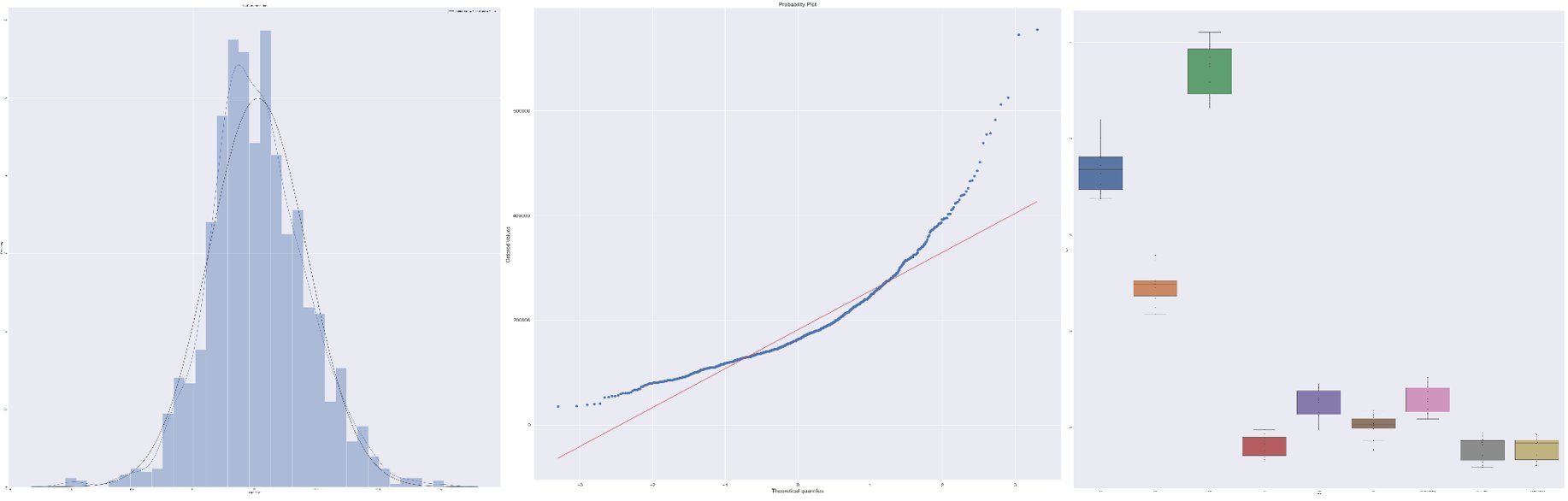
 (Expected Daily Return μ = 0%, Return Standard Deviation σ = 1% )
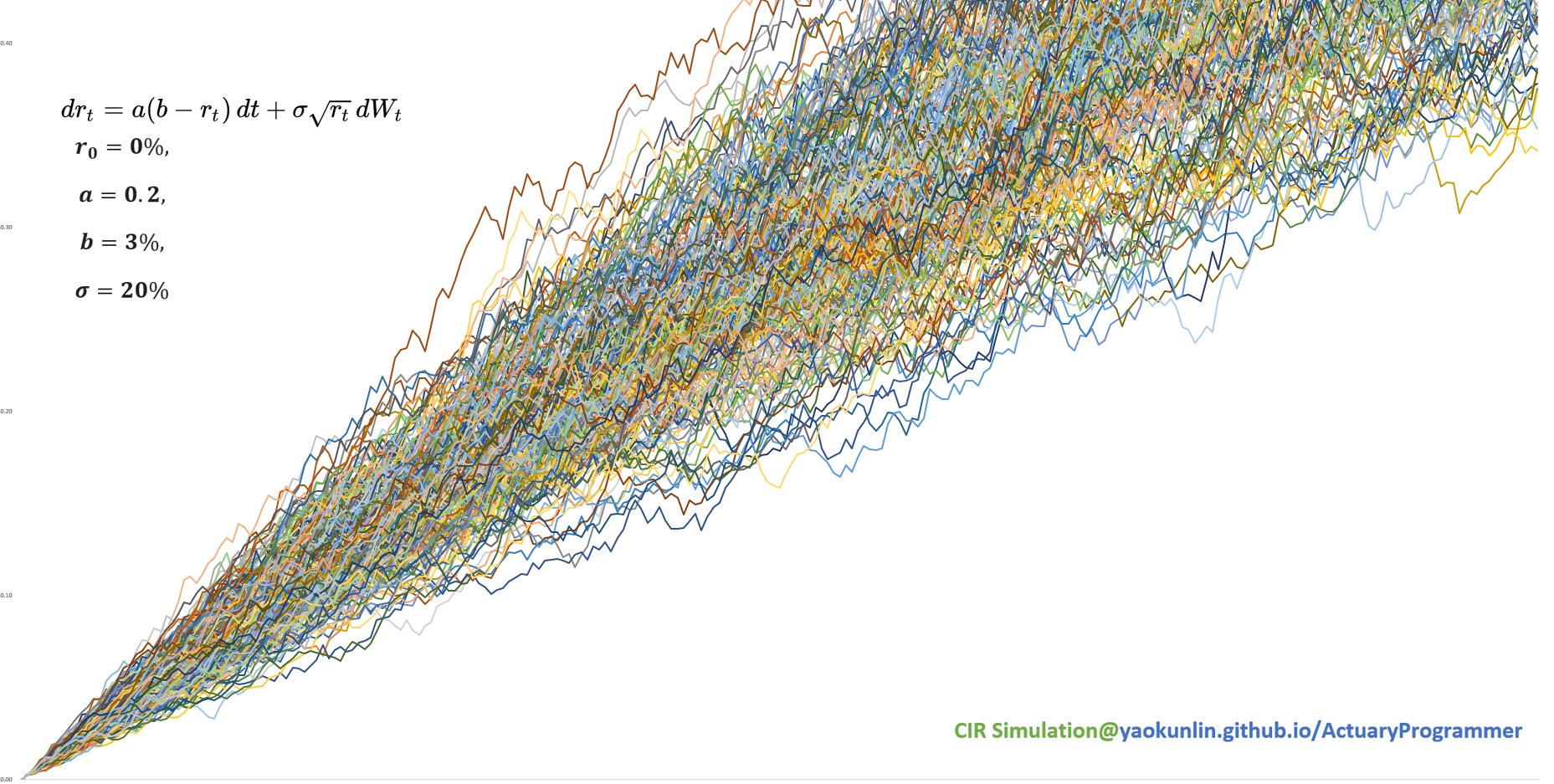
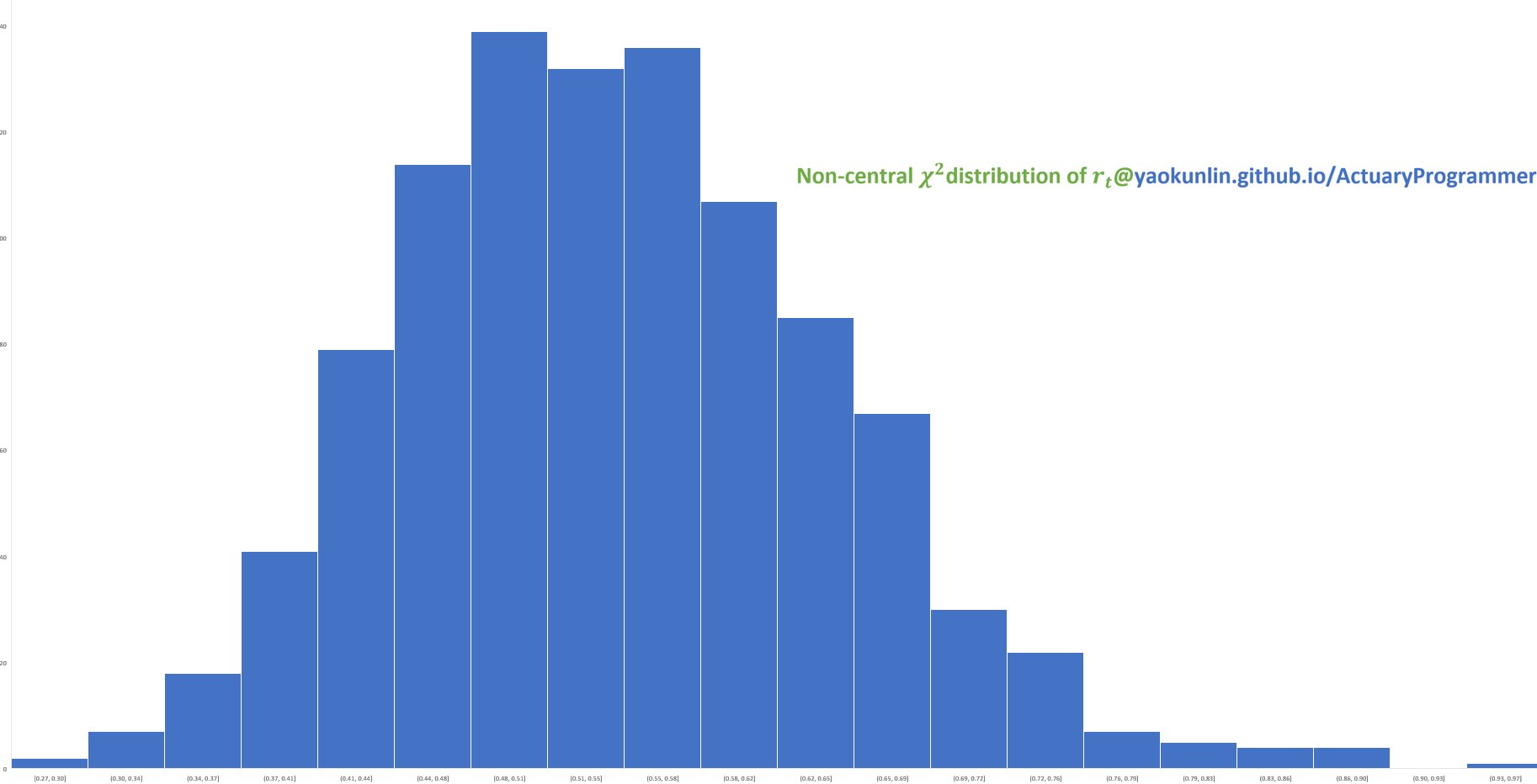
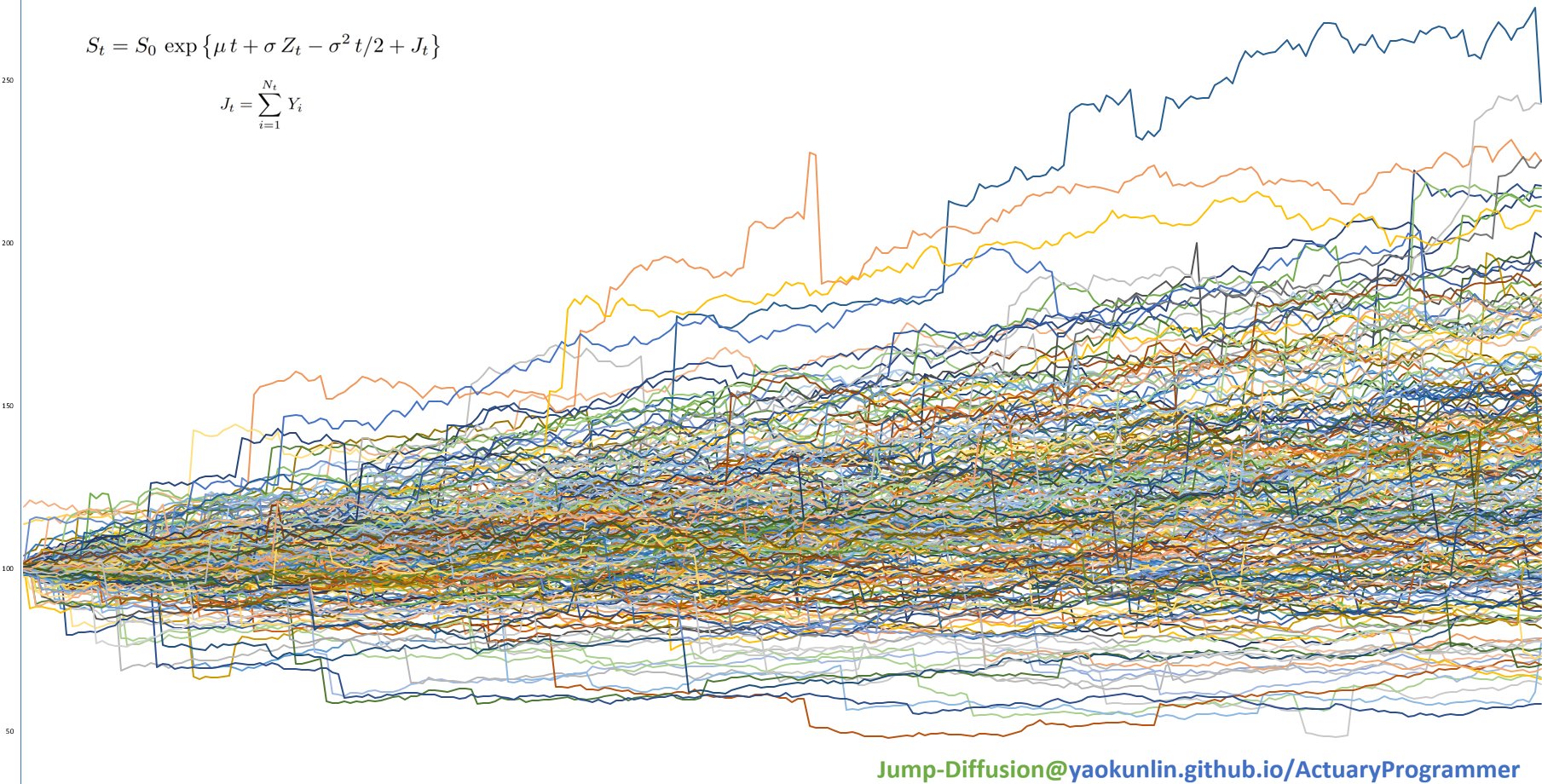
(Expected Daily Return μ = 0%, Return Standard Deviation σ = 1% )